Voir derrière un obstacle est devenu un peu plus possible...

Les réflexions diffuses permettent de reconstituer une image de ce qu'il y a derrière un obstacle.

Voir derrière un obstacle parait impossible - avec notre équipement sensoriel en tous cas. Cependant  Liu, X., et al. (2019)  montrent que puisque la lumière diffuse et peut revenir de derrière l'obstacle, si on illumine avec un faisceau laser pulsé qui balaye une paroi  latérale (mur relais) qui réfléchit ce faisceau vers les objets (Cf Fig 1.a), on peut mesurer les réflexions pulsées qui reviennent des objets et rebondissent sur  cette paroi vers la caméra. Cf Fig 1b. 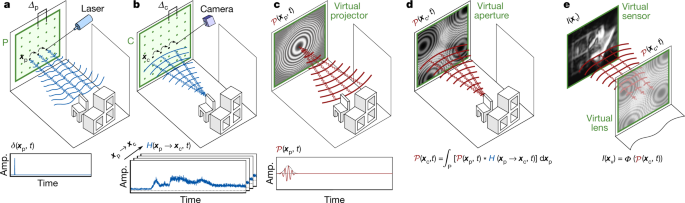Puis à partir de ces nombreuses images réfléchies diffusément on peut reconstituer par calcul (Cf Fig 1.c-d-e)l'image complète y compris ce qui est derrière l'obstacle.

Fig 1: a, b, Capture de données de scène. a, un laser pulsé balaye séquentiellement une paroi de relais (verte); b, la lumière réfléchie par la scène sur le mur est enregistrée au niveau du capteur, produisant une réponse impulsionnelle H de la scène. c, source de lumière virtuelle. L'onde de champ de phaseur d'une source lumineuse virtuelle 𝒫 (𝑥p, 𝑡) est modélisée d'après le front d'onde de la source lumineuse du système LOS modèle. d, la réponse de la scène à cet éclairage virtuel 𝒫 (𝑥c, 𝑡) est calculée en utilisant H. e, la scène est reconstruite à partir du front d'onde 𝒫 (𝑥c, 𝑡) en utilisant la théorie de la diffraction des ondes. La fonction Φ (·) est également extraite du modèle de système LOS. Amp., Amplitude du champ phaseur. [img] source :  Liu, X., et al. (2019)

Abstract de Liu, X., et al. (2019)

L'imagerie sans ligne de visée permet aux objets d'être observés lorsqu'ils sont partiellement ou totalement occultés de la vue directe, en analysant les réflexions diffuses indirectes sur une surface de relais secondaire (relay surface). Malgré de nombreuses applications potentielles les méthodes existantes, les applications  pratique restent lointaines en raison de limitations conceptuelles.

Les auteurs évoquent notamment l'hypothèse d'une seule diffusion, d'une réflectance diffuse idéale et d'un manque d'occlusions dans la scène cachée. En revanche, les systèmes d'imagerie en ligne de visée n'imposent aucune hypothèse sur la scène imagée, bien qu'ils s'appuient sur des processus mathématiquement simples de propagation d'onde diffractive linéaire. Ici, nous montrons que le problème de l'imagerie sans visibilité directe peut également être formulé comme un problème de propagation d'onde diffractive, en introduisant un champ d'onde virtuel que nous appelons le champ de phaseur. Les scènes sans visibilité directe peuvent être imagées à partir de données brutes de temps de vol en appliquant les opérateurs mathématiques qui modélisent la propagation des ondes dans un système d'imagerie en visibilité directe conventionnel. Notre méthode produit une nouvelle classe d'algorithmes d'imagerie qui imitent les capacités des caméras en ligne de visée. Pour démontrer notre technique, nous dérivons trois algorithmes d'imagerie, modélisés d'après trois systèmes de visibilité directe différents. Ces algorithmes reposent sur la résolution d'une intégrale de diffraction d'onde, à savoir l'intégrale de diffraction de Rayleigh – Sommerfeld. Des solutions rapides à la diffraction de Rayleigh – Sommerfeld et ses approximations sont facilement disponibles, ce qui profite à notre méthode. Nous démontrons l'imagerie sans visibilité directe de scènes complexes avec une forte diffusion multiple et une lumière ambiante, des matériaux arbitraires, une large plage de profondeur et des occlusions. Notre méthode gère ces cas difficiles sans inverser explicitement un modèle de transport de lumière. Nous pensons que notre approche contribuera à libérer le potentiel de l'imagerie sans visibilité directe et à promouvoir le développement d'applications pertinentes non limitées aux conditions de laboratoire.

encourage le lecteur à aller vérifier dans l’article d’origine : Liu, X., et al. (2019) ici

Une nouvelle approche algorithmique rend le problème soluble.

Liu, X., et al. (2019) ont développé un nouvelle approche conceptuelle et des algorithmes qui facilitent le calcul de l'image à partir des décalages temporels dans la propagation des ondes de réflexions diffuses- en considérant le mur relais comme une sorte de projecteur puis d'objectif et de senseur de très grande ouverture, les algorithmes s'inspirent de ceux d'une caméra "line-of-sight" et deviennent bien plus simples ( enfin ... moins complexes)  .

 Here we show that the problem of non-line-of-sight imaging can also be formulated as one of diffractive wave propagation, by introducing a virtual wave field that we term the phasor field. Non-line-of-sight scenes can be imaged from raw time-of-flight data by applying the mathematical operators that model wave propagation in a conventional line-of-sight imaging system. Our method yields a new class of imaging algorithms that mimic the capabilities of line-of-sight cameras. Liu, X., et al. (2019)

encourage le lecteur à aller vérifier dans l’article d’origine : Liu, X., et al. (2019) ici

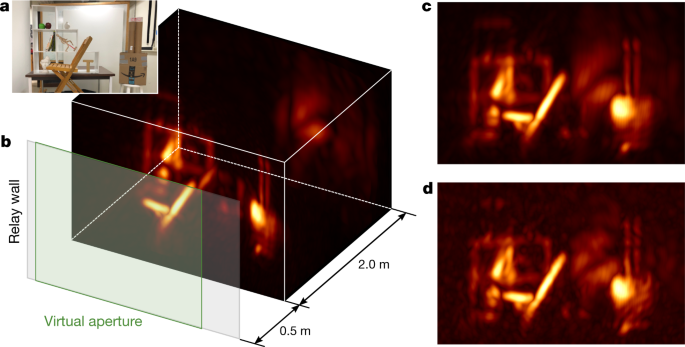
Fig 2: a, Photographie de la scène vue depuis le mur relais. La scène contient des géométries occlusales, avec des objets vers l'avant (comme la chaise) qui cachent partiellement les objets plus en arrière; plusieurs réflectances de surface anisotropes, une grande profondeur de champ et une forte lumière ambiante et à diffusion multiple. b, visualisation 3D de la reconstruction avec des champs de phaseurs (λ = 6 cm). Nous incluons l'emplacement du mur de relais et la couverture de l'ouverture virtuelle à des fins d'illustration. c, vue frontale de la scène, capturée avec un temps d'exposition de 10 ms par position laser. d, vue frontale capturée avec un temps d'exposition de seulement 1 ms (24 s pour le balayage complet). [img]. Source : Liu, X., et al. (2019) ici

Vérification de la robustesse

Liu, X., et al. (2019) ont testé la robustesse de cette technique en pleine lumière,  et avec une très forte profondeur de champ cf figure 3.

Fig. 3 : Evaluation de la robustesse de la technique. a, Reconstruction en présence d'une illumination ambiante forte. b, Scène cachée avec une grande profondeur de champ, impliquant des signaux très faibles des objets plus lointains.  [img]. Source : Liu, X., et al. (2019)

(Les membres Expériment@l-Tremplins peuvent obtenir ces articles…).

Références:

• Liu, X., Guillén, I., Manna, M. L., Nam, J. H., Reza, S. A., Le, T. H., … Velten, A. (2019). Non-line-of-sight imaging using phasor-field virtual wave optics. Nature, 572(7771), 620‑623. https://doi.org/10.1038/s41586-019-1461-3