Flottaison vs viscosité : Archimède renversé ?

Archimède : Une recherche bouscule les limites de ce modèle classiquement enseigné…

La "loi" d'Archimède détermine l'intensité de la force qui permet la flottaison… Or une recherche récente la présente dans les news de Science (Gent, E. 2020) comme remis en question. Les enseignants savent bien que c'est un modèle, qui a son domaine validité, et ses limites. D'un autre côté, le contexte scolaire exige une clarté sur les attentes aux examens. Cette publication Jump-To-Science présente la version vulgarisée, en repère quelques transpositions et renvoie vers toute la richesse de l'article d'origine (Apffel, et al., 2020). Elle discute finalement comment gérer cette tension entre a) les besoins des élèves que rassurent les vérités simples d'un modèle classiquement enseigné et b) la nature hypothétique et la portés de ces modèles quand une recherche récente en révèle les limites.

En effet dans le modèle d'Archimède les forces de viscosité sont négligées, et avec des objets de la taille d'un savant de l'antiquité  elles sont sans doute négligeables.

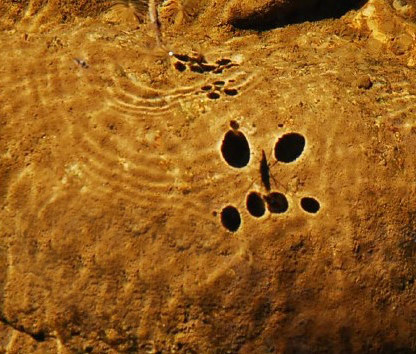
Fig. 1 : Les Gerris  révèlent un équilibre entre les forces de viscosité et de gravitation [img]. Image : Lombard, F.

Par contre ces forces ne sont pas négligeables pour le Gerris lacustris (parfois appelé punaise d'eau ou improprement araignée d'eau) : ses pattes hydrophobes s'appuient, grâce à la tension de surface, sur une dépression de l'eau qui produit la force nécessaire à les tenir au-dessus de la surface de l'eau.  Voir vidéo.

Fig. 2 : il faut prendre en compte la viscosité et la tension de surface pour expliquer le rebond de la goutte. Image : Lombard, F.

Sans prendre en compte la viscosité on ne peut guère expliquer les magnifiques formes des gouttes qui rejaillissent de l'eau. La loi d'Archimède ne serait-elle pas une loi absolue  ? 

L'eau qui s'égoutte : la gravitation et la viscosité, la tension de surface ?

Les gouttes qui se forment les jours de pluie sous un rebord ou sous un robinet restent d'abord attachées à la surface mouillée par des forces liées à la viscosité et la tension de surface, retenant en quelque sorte l'eau, puis la gravitation l'emporte et la goutte tombe. Cf. fig. 3 et  vidéo

Fig. 3 : Les gouttes manifestent un équilibre entre les forces de viscosité, tension de surface et de gravitation. Image et video : Lombard, F.

Ce phénomène est bien connu. Cependant une publication récente (Apffel, et al., 2020) montre que , dans certaines circonstances; si on agite la surface d'un liquide très visqueux, la goutte est réabsorbée avant d'avoir pu se détacher, et  Gent, E. (2020) explique que des objets paraissent flotter à l'envers sous la surface inférieure du liquide .  

Fig 4: Cliquer pour animer. Agité énergiquement le liquide visqueux empêche les petits objets de tomber ou de remonter vers la surface supérieure [img]. Source : Gent, E. (2020) d'après Apffel et al., 2020

Des bateaux en lévitation semblent renverser la loi d'Archimède

Gent, E. (2020) dans une News de Science ici commente une étude où l'équipe d'Emmanuel Fort, à l'ESPCI  (Apffel, et al., 2020) ici a réussi à faire flotter de minuscules bateaux sur la face inférieure d'une couche de liquide (voir animation ci-dessus). Gent, E. (2020) évoque avec humour des possibilités nautiques inhabituelles, mais ces résultats sont troublants pour la compréhension naïve de la flottabilité. On observe ici que la vulgarisation met en évidence une conclusion accrocheuse.

Le modèle utilisé pour expliquer pourquoi les bateaux flottent est resté en grande partie inchangé depuis que le mathématicien grec antique Archimède a expliqué comment la force de gravité descendante est équilibrée par la pression ascendante de l'eau déplacée. ent, Gent, E. (2020) indique que les vibrations peuvent induire un comportement étrange qui semble défier la gravité. En ébranlant un modèle solaire bien établi, on voit de nouveau que la vulgarisation met en évidence un aspect accrocheur apparemment issu des conclusions de cette recherche.

En 1951, le physicien russe Piotr Kapitza, lauréat du prix Nobel, a décrit comment le fait de secouer rapidement un pendule inversé le stabilise plutôt que de le faire basculer vers sa position stable naturelle : Kapitza effect, which is the dynamical stabilization of an inverted pendulum by vertical shaking dit l'article d'origine.  Depuis lors, les scientifiques ont utilisé les vibrations pour faire léviter des liquides dans les airs et faire couler plutôt que de monter des bulles d'air (Cf. p. ex. Krieger, 2017). Cette nouvelle étude suggère qu'ils peuvent également inverser les règles de flottabilité. Traduction, d'après Gent, E. (2020). encourage le lecteur à aller vérifier dans l'article d'origine :  ici

Avant qu'une goutte se forme, la secousse (et la viscosité) fournit une force opposée qui la rappelle

Des expériences antérieures avaient montré que les fluides visqueux dans un conteneur vibrant peuvent être amenés à léviter. C'est parce que chaque fois qu'une partie du liquide essaie de s'égoutter, la secousse fournit une force opposée qui le retient. Cela empêche la surface inférieure du fluide de se briser et emprisonne un coussin d'air en dessous. Traduction d'après Gent, E. (2020). Mais Emmanuel Fort, dont le laboratoire se concentre sur l'optique et l'imagerie, n'était pas au courant de ces recherches antérieures. Avec ses collègues, ils se sont inspirés du pendule de Kapitsa  pour voir s'ils pouvaient reproduire un comportement similaire dans un liquide. Ils ont construit un récipient en plexiglas sur une machine à secouer et l'ont rempli de liquides visqueux tels que de l'huile de silicone ou du glycérol. Ensuite, ils ont utilisé une aiguille pour injecter une couche d'air au fond et ont vu que le liquide vibrant lévitait au-dessus.  
Pour bien comprendre le dispositif expérimental il faut se référer à l'article d'origine : Apffel, et al. (2020), Jump-To-Science en a extrait la figure 6 ci-dessous.

Fig 6: a, Montage expérimental, composé d'un récipient en plexiglas  (jusqu'à 20 cm de largeur) fixé sur un agitateur oscillant verticalement avec amplitude A et fréquence ω / (2π). Le liquide est soit du glycérol ou de l'huile de silicone à haute viscosité (typiquement 0,5 Pa s). Les bulles sont créées en injectant de l'air avec une seringue à travers une longue aiguille. L'expérience se déroule à température ambiante (20 ° C). b, Séquence d'images (de gauche à droite, de haut en bas) de la création de la couche d'air obtenue en injectant avec une aiguille de l'air au fond du bain liquide oscillant. La bulle qui coule grandit jusqu'à ce qu'elle remplisse complètement le fond du récipient (voir les vidéos supplémentaires 1, 2). c, d, Amplitude verticale de la couche liquide, Al / A (c), et le déphasage relatif ϕl - ϕ des oscillations du liquide par rapport à celui du secoueur (d) en fonction de la fréquence d'excitation ω / (2π ). En médaillon, schéma du système masse-ressort composé de la couche d'air chargée du liquide en lévitation (c) et image de l'instabilité de Faraday qui se déclenche sur les deux surfaces opposées de la couche liquide en lévitation d'huile de silicium (d; voir Vidéo supplémentaire 3). Les données expérimentales (cercles pleins) sont ajustées par le modèle ressort-masse avec les paramètres d'ajustement ω / (2π) = 103 Hz et Γ = 0,04 (ligne pointillée; voir les supplementary informations pour plus de détails). e, vues de trois quarts colorisées numériquement des conteneurs oscillants avec une et deux couches liquides de lévitation d'huile de silicone (voir vidéo supplémentaire 4). f, Haut, vues latérales colorisées numériquement du bain de lévitation dans des récipients de largeurs L = 2 cm (gauche) et L = 18 cm (droite); voir Vidéo supplémentaire 5. Bas, vitesse critique du liquide 𝑣 ∗ l = Alω pour la stabilisation de Kapitza de la couche liquide en fonction de la largeur L du conteneur: données expérimentales (cercles) et modèle 𝑣 ∗ l = 𝑔𝐿 / 𝜋‾‾‾ ‾‾√ (ligne pointillée). Les barres d'erreur correspondent aux valeurs extrêmes sur cinq expériences.  [img]. Source :Apffel et al. (2020) Notre traduction

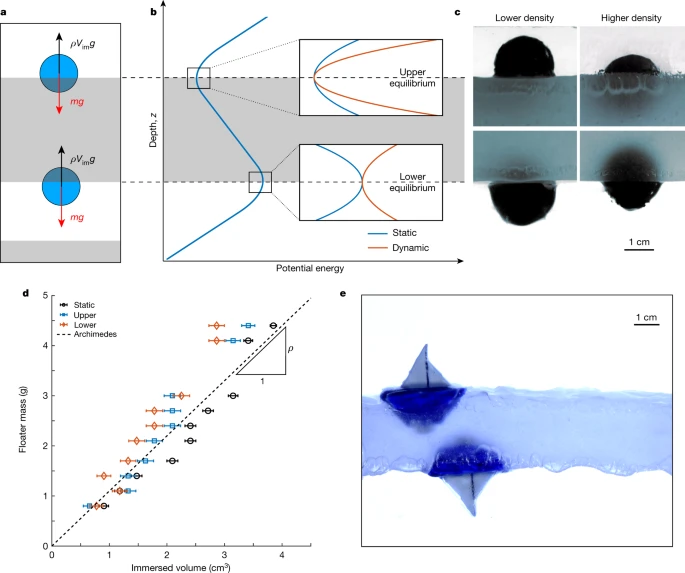
Après avoir réalisé que le phénomène avait été documenté il y a des décennies, Apffel et al. (2020) ont peaufiné l'expérience en plaçant de petites perles dans la couche de liquide en lévitation - et ont vu qu'elles flottaient de manière stable sur la face inférieure du liquide. «C'était complètement inattendu», déclare Emmanuel Fort dans la news de Gent, E. (2020).  Cf. figure 6. On observe ici que la vulgarisation propose la réaction personnelle qui souligne la dimension inattendue et peut avoir un effet accrocheur.

.

Pour accroitre l'impact visuel (un pied de nez aux cours de physique trop dogmatiques ?), Apffel et al. (2020) ont échangé les perles contre de petits modèles de bateaux et ont découvert qu'ils pouvaient flotter sur les surfaces supérieure et inférieure en même temps. Cf. figure 4. encourage le lecteur à aller vérifier dans l'article d'origine :  ici

Apffel et al. (2020) présentent un modèle pour expliquer comment les effets de la flottabilité se reflètent sur la face inférieure du fluide, dans un article au titre percutant :Floating under a levitating liquid". Normalement, de légères perturbations devraient pousser l'objet soit vers le bas dans l'air libre, où il tomberait… soit vers le haut dans le liquide où la flottabilité prendrait le dessus et le pousserait vers le haut. Mais de fortes vibrations peuvent annuler ces perturbations. Elles maintiennent l'objet stable sur la surface inférieure où la traction vers le bas de la gravité et la traction vers le haut de la flottabilité sont parfaitement équilibrées, explique Gent, E. (2020). 
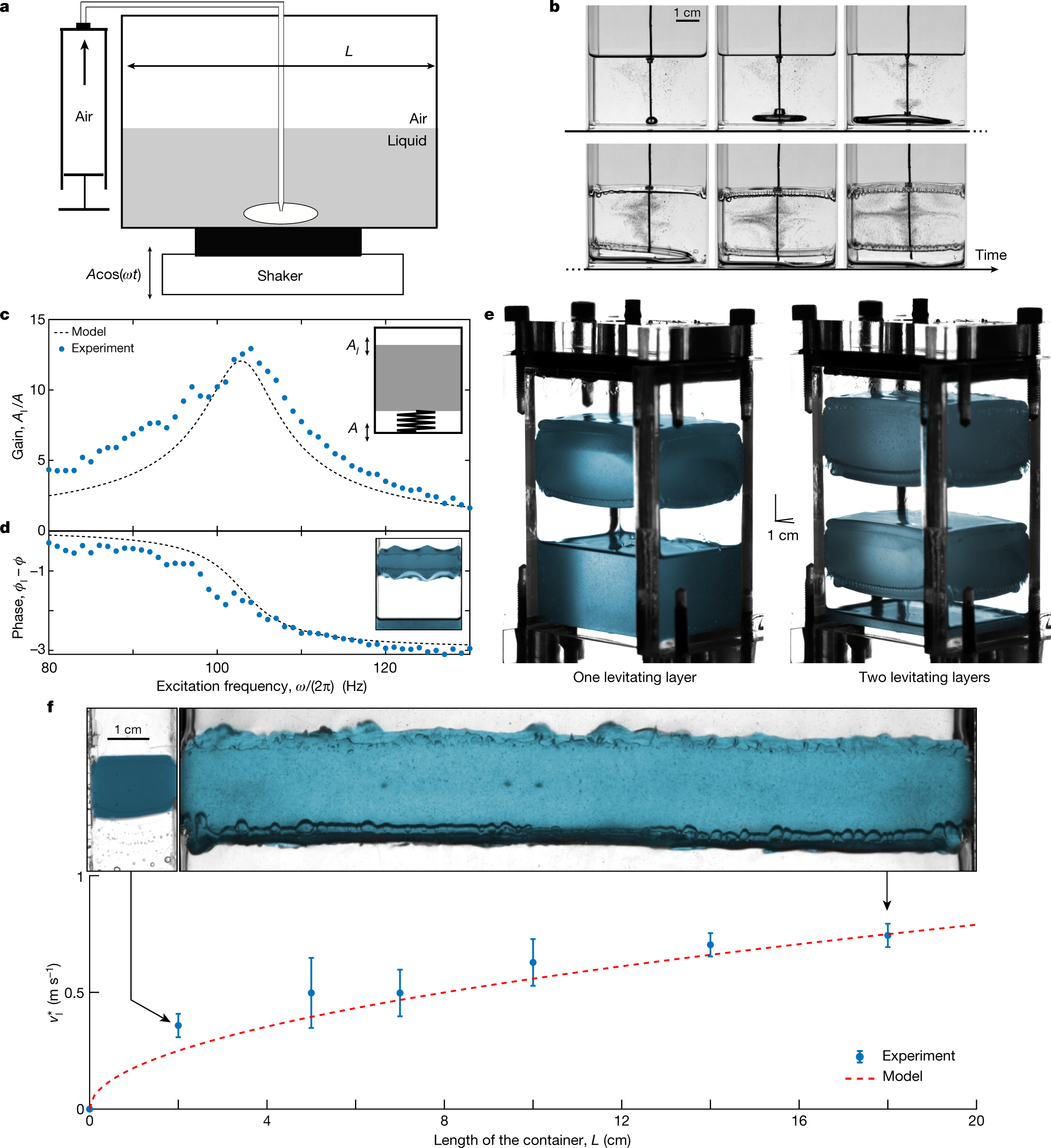
Pour bien comprendre ce modèle, il faut se référer à l'article d'origine. Jump-To-Science en a extrait la figure 7 ci-dessous... mais encourage chacun.e à se faire plaisir en lisant l'original ici

Fig 5: a, Schéma de l'équilibre des forces aux deux interfaces opposées; la force de flottabilité annule le poids des corps immergés, où V_im est le volume immergé. b, Profil typique du potentiel statique (bleu) le long de la direction verticale z en négligeant les effets dynamiques. Deux positions d'équilibre apparaissent à chaque interface; l'équilibre inférieur est instable. Encarts, grossissements du potentiel à proximité des positions d'équilibre avec ajout de l'effet de stabilisation dynamique (ligne rouge; voir Informations complémentaires). c, Vues latérales colorisées numériquement de sphères en plastique de 2 cm de diamètre, flottant vers le haut et vers le bas avec une densité inférieure (gauche) et supérieure (droite). d, Positions d'équilibre moyennées dans le temps pour des sphères de 2 cm de diamètre avec des masses variables, en fonction du volume immergé à l'interface supérieure (carrés bleus) et à l'interface inférieure (losanges rouges). Les cercles noirs donnent les positions d'équilibre obtenues sans secousse. La ligne en pointillé est donnée par le principe d'Archimède avec  ρ_l  mesuré expérimentalement = 1.1 kg l⁻¹ pour le glycérol. Les barres d'erreur correspondent à des valeurs extrêmes sur trois mesures. e, Bateaux flottant au-dessus et au-dessous d'une couche de liquide en lévitation (voir la vidéo supplémentaire 6; coloriée numériquement). [img]. Source :Apffel, et al. (2020).

On ne sait pas encore si ce dispositif fascinant a des utilisations pratiques. Des vibrations ont été utilisées pour contrôler le mouvement des bulles dans les fluides pour le traitement des minéraux et les réactions chimiques, mais Gent, E. (2020)  s'interroge sur les utilités de cette nouvelle découverte: la plus grande contribution, ajoute-t-il, est de montrer que les systèmes vibrants détiennent encore des comportements exotiques non découverts.

Le dispositif expérimental de l'équipe n'a été testé qu'avec demi-litre de liquide au maximum, mais leurs équations suggèrent que la seule limite à ce volume est la puissance de la machine à secouer. Et si l'approche fonctionne bien avec des liquides visqueux, elle ne fonctionne pas aussi bien avec de l'eau, selon E. Fort. (l'eau n'est pas visqueuse et n'a pas une tension de surface liquide-liquide très importante)
"A moins que vous ne soyez heureux de vous lancer dans une mer d'huile minérale visqueuse, les rêves de navigation à l'envers pourraient le rester", s'amuse Gent, E. (2020).
On voit de nouveau que la vulgarisation extrapole un aspect accrocheur des conclusions de cette recherche. C'est classiquement ce qui se passe dans la vulgarisation .

Il apparait clairement que pour comprendre les méthodes et le dispositif expérimental il faut se référer à Apffel, et al., (2020). encourage le lecteur à aller vérifier dans l'article d'origine :  ici

La comparaison avec l'article d'origine, là où les savoirs scientifiques sont produits révèle bien ce qui disparait (les méthodes, les limites, le degré de certitude,les modèles formalisés…) et ce qui est mis en avant : les conclusions accrocheuses, l'évolution de modèles à la protée plus large et délimitant mieux les limites des précédents, présenté un peu comme une remise en question d'une vérité établie (Green Staerklé, et al (2002).

Faut-il semer le doute dans l'esprit des élèves en évoquant ces limites du modèle d'Archimède ?

On pourrait craindre que ces recherches conduisent à douter du bien fondé de l'enseignement de la science (physique, ici) : "mais alors la loi d'Archimède est même pas vraie, m'dame/ m'sieur ! … ça sert à quoi de l'apprendre ?" 

L'enseignement des sciences ne peut éviter d'affronter une tension entre a) les exigences de clarté sur ce qui sera demandé à l'évaluation (et donc sur les objectifs) et b) le constat que les savoirs scientifiques sont établis sur la base de modèles qui ne sont pas des certitudes mais des "simplifications de phénomènes focalisées sur certaines caractéristiques et qui peuvent être utilisés pour produire des explications d'observations et mesures ainsi que des prédictions": 

"A scientific model is an abstract, simplified, representation of a system of phenomena that makes its central features explicit and visible and can be used to generate explanations and predictions "(Harrison & Treagust, 2000)ici

Ainsi il n'y a pas en sciences de Top-modèle  (cf Jump-To-Science 2011) qui serait tout simplement vrai, mais des modèles pertinents pour certains problèmes dans certains contextes.

"La question est alors non pas : quel bon modèle enseigner ?
Mais : comment donner aux modèles manipulés leurs trois caractéristiques essentielles :

• ils sont hypothétiques
• ils sont modifiables
• ils sont pertinents pour certains problèmes dans certains contextes ?" Martinand, J. L. (1996)

Résoudre cette tension inévitable dans le monde scolaire ?

Cette tension entre le a) besoin pédagogique de clarté, de certitude pour les élèves de ce qu'il faut savoir et savoir faire pour avoir une bonne note d'une part et b) la nature hypothétique et l'incertitude délimitée des savoirs de la science est incontournable.
Le modèle d'Archimède n'était pas simplement vrai avant Apffel,et al.(2020), il n'est pas faux depuis ces recherches.  Son domaine de validité et les problèmes pour lesquels il est pertinent sont mieux définis.

Cela n'empêche pas de clarifier dans un contexte scolaire qu'en vue de l'examen le modèle d'Archimède, de Mendel, ou un autre est celui que les élèves doivent savoir utiliser pour obtenir la note maximale. Rien n'empêche alors d'aider les élèves à voir les limites du modèle institutionnalisé, son domaine de validité, le type de problèmes pour lesquels il est pertinent ou non.

Et les articles vulgarisés par leur côté accrocheur sans donner les réponses scientifiques pourraient être utilisés pour susciter des questions, donner envie de savoir comment ces savoirs ont été produits ?

Pour aller plus loin …

Peut-on travailler avec les élèves une progression vers un usage moins naïf des modèles ? Schwarz, et al. (2009) suggèrent que c'est possible : cf ici.

Ce serait cohérent avec la place centrale des modèles dans les plans d'études PER (CIIP, 2011)

Références:

• Apffel, B., Novkoski, F., Eddi, A., & Fort, E. (2020). Floating under a levitating liquid. Nature, 585(7823), 48‑52. https://doi.org/10.1038/s41586-020-2643-8
• CIIP, (2011). Plan d'études Romand. Romandie, Suisse: Conférence intercantonale de l'instruction publique de la Suisse Romande et du Tessin.ici
• Gent, E. (2020). Watch levitating upside-down boats flip the law of buoyancy. Science. https://doi.org/10.1126/science.abe6164
• Green Staerklé, E., & Clémence, A. (2002). De l'affiliation des souris de laboratoire au gène de la fidélité dans la vie : Un exemple de transformation du savoir scientifique dans le sens commun. In C. Garnier & W. Doise (Éds.), Représentations sociales. Balisage du domaine d'études. Montréal : Éditions nouvelles, pp. 147—155, 2002. (p. 147‑155). intranet.pdf
• Harrison, A. G., & Treagust, D. F. (2000). A typology of school science models. International journal of science education, 22(9), 1011‑1026. https://doi.org/10.1080/095006900416884
  
• Kapitza, P. L. (1951). Dynamic stability of a pendulum with an oscillating point of suspension. Journal of experimental and theoretical physics, 21(5), 588‑597.
• Krieger, M. S. (2017). Interfacial fluid instabilities and Kapitsa pendula. The European Physical Journal E, 40(7), 67. https://doi.org/10.1140/epje/i2017-11556-x
• Martinand, J.-L. (Dir.) (1992). Enseignement et apprentissage de la modélisation en sciences. Paris, INRP
• Martinand, J. L. (1996). Introduction à la modélisation. Actes du séminaire de didactique des disciplines technologiques., Cachan  Paris | . pdf
  
• Martinand, J. L. (2010). Schémas didactiques pour la modélisation en sciences et technologies. Spectre, 40, 1, 20‑24. intranet.pdf
• Schwarz, C., Reiser, B. J., Davis, E. A., Kenyon, L., Achér, A., Fortus, D., Shwartz, Y., Hug, B., & Krajcik, J. (2009). Developing a learning progression for scientific modeling : Making scientific modeling accessible and meaningful for learners. Journal of Research in Science Teaching, 46(6), 632‑654. https://doi.org/10.1002/tea.20311
  

--