Peut-on "voir" des couleurs invisibles ?

Voir l'invisible… un oxymore ou un paradoxe à découvrir ?

Des recherches récentes remettent en question ce que nous pensons être indiscutable : ce que nous voyons !
On sait la difficulté des élèves - dans les labos ou TP - à voir ce qui nous paraît évident et à rejeter ce qui ne rentre pas dans leurs schémas de pensée. 

"L'élève ne croit pas ce qu'il voit, il voit ce qu'il croit"
…trouvé chez plusieurs chercheurs dont Giordan et Astolfi probablement repris de Gaston Bachelard, dans La formation de l'esprit scientifique (1938) « Rien ne va de soi. Rien n'est donné. Tout est construit. »

Ces publications aideront peut-être vos élèves à se décentrer de leurs impressions et perceptions du monde... une compétence indispensable en science et peut-être aussi dans un monde où nos perceptions superficielles projetées sur les autres contribuent à bien des conflits.

A) Une première publication, (Ma, et al., 2025) décrit comment des chercheurs ont réussi avec des lentilles munies de composites de nanoparticules à absorber de l'infrarouge (invisible pour nos yeux, donc) pour le ré-émettre dans le visible. encourage le lecteur à aller vérifier dans l'article d'origine :  ici

B) Une deuxième publication (Gibney, E., 2025) rapportent  dans une news de Nature comment Fong, …, Ng,et al. (2025) ont réussi à balayer la rétine au fond de loeil de 5 sujets en illuminant les cônes "verts" seulement, produisant la sensation d'une couleur qui ne peut être vue naturellement encourage le lecteur à aller vérifier dans la news d'origine :  ici

C) Une troisième publication (Sara Reardon, 2024) décrit comment  équipe de spécialistes des matériaux (Ou, et al. 2024) sont parvenus à rendre temporairement transparente la peau de souris révélant ainsi les organes sous-jacents. Simplement en  appliquant un pigment courant, la tartrazine, l'un de ceux qui donnent leur couleur orange caractéristique aux célèbres snacks Cheetos. encourage le lecteur à aller vérifier dans la news d'origine :  ici

A) Des lentilles pour voir une partie de l'infrarouge

Les humains ne perçoivent pas la lumière infrarouge en raison des propriétés de l'œil. Pourtant, la capacité de voir à l'œil nu cette lumière invisible serait extrêmement précieuse dans de nombreux contextes. Dans cet article, les auteurs présentent des lentilles de contact infusées de nanoparticules capables de convertir la lumière proche infrarouge (NIR) 800–1,600 [nm] en signaux visibles 400–700[nm]. Ces lentilles, souples, compatibles avec l'œil humain et confortables à porter, ont permis à des d'identifier des informations spatiales et temporelles en NIR et de réagir en conséquence.
Équipés de telles lentilles, des participants humains ont pu distinguer des signaux codés en NIR, à la fois sous forme de séquences temporelles et d'images spatiales. Les chercheurs ont aussi mis au point une version trichromatique de ces lentilles, permettant de percevoir différentes "couleurs" dans le NIR, ouvrant ainsi la voie à une véritable vision colorée spatio-temporelle dans ce spectre invisible. Cette recherche ouvre des perspectives pour le développement de matériaux portables permettant une vision infrarouge non invasive, et pour de nouvelles manières de percevoir et de communiquer des informations au-delà du spectre visible. Ils notent que l'IR passe bien à travers les paupières et qu'on pourrait ainsi transmettre discrètement des informations à des yeux fermés.
D'autres on même proposé même que des variantes de ces lentilles les aident à distinguer des nuances de rouge, qui seraient converties en nuances de couleurs qu'ils voient. Traduction IA retouchée de Ma, et al. (2025) encourage le lecteur à aller vérifier dans l'article d'origine :  ici

 
Fig 1: Abstract visuel de l'article dans Cell Source : Ma, et al. (2025)

Convertir des photons IR vers le visible, d'où vient l'énergie ... ???

Cette upconversion est un mécanisme comparable à la fluorescence mais inverse (des photons de plus basse énergie (IR) sont convertis en photons d'énergie plus élevée (visible ). Or "Tous les matériaux fluorescents obéissent en général au principe bien connu de la loi de Stokes, qui énonce simplement que les photons d'excitation possèdent une énergie plus élevée que les photons émis. En d'autres termes, l'énergie des photons émis est inférieure à celle des photons absorbés. Cela revient, de manière indirecte, à exprimer que le rendement énergétique ne peut pas dépasser 1. Ce principe reste bien sûr valable uniquement lorsqu'on considère un système où un seul ion est excité." Traduction de  Auzel, F. (2004) ici  encourage le lecteur à aller vérifier dans l'article d'origine ici

L'upconversion photonique (ou "conversion ascendante") : plusieurs photons d'énergie plus basse (ex : infrarouge) sont absorbés de manière coopérative ;et leur énergie est "additionnée" par des mécanismes non linéaires ; puis un photon d'énergie plus élevée (ex : lumière visible) est émis.
    → ici, on a un décalage vers le bleu (longueurs d'onde plus courtes). Voir notamment Auzel, F. (2004)   encourage le lecteur à aller vérifier dans l'article d'origine notamment la section 2.2 "Upconversion Processes by Sequential Energy Transfers "

Des limites :

Certains chercheurs restent sceptiques quant à l'intérêt pratique de ces lentilles. « Je ne vois pas d'application qui ne serait pas plus simplement réalisable avec des lunettes infrarouges », commente Glen Jeffery, neuroscientifique à l'University College de Londres, spécialiste de la santé de l'œil. « Si l'évolution n'a pas retenu ce type de mécanisme de vision, c'est probablement pour de bonnes raisons. ».
Une formulation que vos élèves, critiques et bien formés à la pensée évolutive, reformuleront d'un air narquois : « Ce type de mécanisme de vision n'a pas été sélectionné au cours de l'évolution, ce qui signifie probablement qu'il engendre davantage de coûts ou de contraintes que d'avantages sélectifs. »

Applications pour l'enseignement

I) En physique — Ondes et spectres

Pour illustrer le spectre électromagnétique : situer la lumière infrarouge par rapport au visible, et aux  différentes gammes d'ondes (radio, micro-ondes, IR, UV…).

Pour discuter la conservation de l'énergie… en contredisant apparemment la loi de Stokes. L'occasion de rappeler que les lois sont en fait des modèles qui ont un domaine de validité et sont forcément hypothétiques... jusqu'à de nouvelles découvertes qui en redéfinissent les limites - comme ici.

Avec les plus avancés : Interaction onde-matière : comment les nanoparticules de ces lentilles convertissent l'IR en lumière visible ?
Introduction au phénomène de conversion de fréquence : fluorescence, phosphorescence et upconversion photonique

II) En biologie : Susciter des questions sur le fonctionnement de l'œil humain : ce que nos opsines détectent, les spectres de sensibilité des cônes - et l'infrarouge non détecté
cf. par exemple une synthèse assez fouillée de Solomon, et al. (2007) ici

On pourrait envisager de partir de cette recherche - vulgarisée par exemple ici à la RTS - pour discuter les limites de nos perceptions.

Fig 2: Une illustration trouvée dans l'article de la RTS montrant la procédure élaborée par les scientifiques chinois [Sheng Wang][ [img]. Source : Ma, et al. (2025

 Pour les élèves ce qu'ils perçoivent est la vérité. Or la vision est un processus de reconstruction influencé par ce qu'on connaît.  

III) Science-société
Discuter des valeurs morales : faut-il accepter des technologies qui augmentent nos capacités perceptives ou respecter la nature, l'ordre divin, notre héritage génétique ?

De belles discussions en vue

---

B) Percevoir une couleur que personne n'a jamais vue ?

"Imaginez que vous voyez une couleur qu'aucun œil humain n'a encore jamais perçue. C'est ce qu'ont permis des chercheurs en utilisant des lasers et des technologies de suivi oculaire pour stimuler de manière ciblée certaines cellules de la rétine. 

Résultat : cinq volontaires ont vu une teinte bleu-vert d'une intensité inédite, baptisée olo, extrêmement saturé — bien au-delà de ce que permet la vision naturelle.
Fong, …, Ng,et al. (2025) ici:

Une nouvelle couleur créée en illuminant seulement les cônes "verts"  dans l'œil humain avec un laser

Ce n'est pas la première fois que des chercheurs parviennent à stimuler des cônes individuels — ces photorécepteurs de l'œil dont le cerveau décode les signaux en couleurs. Mais c'est la première fois que cette stimulation est réalisée sur une surface suffisante pour modifier de façon significative la perception visuelle. « Ce qui est inédit ici, c'est la démonstration que de telles "nouvelles couleurs" peuvent bel et bien être perçues », souligne Sérgio Nascimento, physicien spécialiste de la vision humaine à l'Université de Minho (Portugal).
Les chercheurs (Fong, …, Ng,et al., 2025), qui ont détaillé leur technique dans Science Advances (avril 2025), ont baptisé cette couleur inédite olo. Elle évoque le bleu paon ou le bleu sarcelle (teal), mais avec un niveau de saturation "hors normes", selon Ren Ng (Université de Californie, Berkeley), co-auteur de l'étude et lui-même l'un des cinq testeurs. encourage le lecteur à aller vérifier dans la news d'origine :  ici

Figure 3 : Le dispositif OZ permettant de stimuler sélectivement les cônes M (verts) : Fong, …, Ng,et al., 2025  [img]

La méthode — surnommée Oz — permet de contrôler précisément les doses de lumière envoyées à chaque cellule de la rétine, de manière à "leurrer" les signaux que le cerveau interprète comme une couleur, ou même à créer des signaux qu'il n'a jamais rencontrés.
Ren Ng précise que cette approche pourrait aussi générer d'autres couleurs inédites. Elle pourrait également, à terme, améliorer la perception des couleurs chez les personnes daltoniennes pour lesquels il n'existe actuellement aucun traitement efficace. Pour l'instant, la technique ne permet de contrôler la couleur que sur une petite portion du champ visuel (environ deux fois le diamètre apparent de la Lune). De plus, elle repose sur des équipements encore rares. Mais même sans applications immédiates, cette avancée est déjà « un véritable exploit technique », selon Jenny Bosten, neuroscientifique à l'Université du Sussex (Royaume-Uni). « Le potentiel pour de futures recherches est immense. » encourage le lecteur à aller vérifier dans la news d'origine :  ici

La vision des couleurs

La vision humaine des couleurs repose sur la comparaison par le cerveau des signaux envoyés par trois types de cônes, chacun sensible à une gamme différente (mais chevauchante) de longueurs d'onde : les cônes S (bleu), M (vert) et L (rouge). Chaque couleur perçue correspond à un "profil d'activation" unique de ces trois types de cônes. Or, en temps normal, toute stimulation du cône M (au milieu du spectre) active aussi, dans une certaine mesure, les cônes voisins S ou L.  cf. les spectres de sensibilité relative des cônes (et des bâtonnets (rods))

cf. par exemple une synthèse assez fouillée de Solomon, et al. (2007) ici et figure ci-contre

L'équipe de Ren Ng s'est donc demandé si une stimulation isolée du cône M pourrait engendrer une nouvelle perception colorée.
Après avoir cartographié précisément la rétine de chaque participant, les chercheurs ont pu cibler des cônes M spécifiques avec des microdoses de lumière laser.
Résultat : les participants ont perçu une couleur olo plus intense que n'importe quel bleu-vert naturel. Pour tenter de la "ramener" dans l'espace des couleurs connues, il a fallu y ajouter de la lumière blanche. encourage le lecteur à aller vérifier dans la news d'origine :  ici

Des sensations de couleurs différentes avec un laser d'une seule couleur

Le système Oz a également permis de générer toute une palette de couleurs en utilisant une seule longueur d'onde de lumière. En modulant l'intensité du laser pour chaque type de cône, les chercheurs ont réussi à reproduire le "schéma d'activation" attendu par le cerveau pour chaque couleur — donnant l'illusion d'une vidéo en couleur, produite à partir d'un seul laser !

Les chercheurs explorent maintenant la possibilité d'adapter cette technologie pour aider les personnes daltoniennes. Chez ces dernières, seuls deux types de cônes fonctionnent correctement. Des travaux antérieurs chez le singe écureuil ont montré qu'un traitement génique peut restaurer la vision des couleurs en ajoutant un troisième type de cône. Ici, l'idée serait de "simuler" ce troisième canal grâce au contrôle laser. « Le cerveau recevrait alors trois types d'informations. Reste à savoir s'il pourrait en faire une vision complète des couleurs », explique Ren Ng.

Au-delà des applications possibles, cette recherche offre un outil unique pour mieux comprendre comment les signaux de la rétine se traduisent en perception colorée dans le cerveau. « Cette technique ouvre des perspectives d'exploration inédites — sans doute plus que tout autre outil utilisable chez l'humain », conclut Kimberly Jameson."
Traduction adaptée de Gibney, E (2025) ici  encourage le lecteur à aller vérifier dans la news d'origine:  ici

---

C) Un colorant alimentaire permet de voir l'intérieur d'une souris

"Dans une news de Science, Sara Reardon (2024) ici décrit une recherche récente :  En général.pour  observer ce qui se passe à l'intérieur du corps, les médecins utilisent toute une gamme de techniques d'imagerie coûteuses : rayons X, échographie, IRM, endoscopie, etc.
Mais une équipe de spécialistes des matériaux (Ou, et al. 2024) a trouvé une approche beaucoup plus simple — du moins chez la souris. En appliquant un pigment courant, ils sont parvenus à rendre temporairement transparente la peau des animaux, révélant ainsi les organes sous-jacents. "
"En plaçant la main devant une lampe, les doigts apparaissent rougeâtre, mais on ne distingue pas les os, les muscles ou les vaisseaux sanguins. Cela s'explique par la diffusion de la lumière dans les tissus biologiques, qui empêche une transmission directe. Cette diffusion est liée à la composition hétérogène des tissus. Chaque matériau transparent possède un indice de réfraction, défini comme le rapport entre la vitesse de la lumière dans le vide et dans le matériau. Par exemple, la lumière se déplace dans l'eau à environ 75 % de sa vitesse dans le vide (indice de 1,33). Lorsque la lumière traverse des matériaux d'indices différents, elle change de direction — le principe même des lentilles optiques. 

Transparence si les milieux ont le même indice de réfraction   

Dans les tissus, les lipides des membranes cellulaires ont un indice d'environ 1,4, supérieur à celui de l'eau environnante. Résultat : les cellules se comportent comme une multitude de petites lentilles désordonnées qui diffusent la lumière dans toutes les directions. Certaines techniques permettent déjà de rendre des tissus — voire des souris entières — transparents, en éliminant les lipides et en ne laissant qu'un gel aqueux, mais ces méthodes détruisent les membranes cellulaires et ne peuvent donc être utilisées sur des animaux vivants.Traduction adaptée de Sara Reardon (2024) ici  encourage le lecteur à aller vérifier dans la news d'origine ici
"Guosong Hong (Ou, et al. 2024) ont cherché à ajuster l'indice de réfraction de l'eau, en l'élevant pour le rapprocher de celui des lipides et des protéines. D'après leurs calculs, un colorant jaune synthétique appelé tartrazine permettait de ralentir la lumière à la vitesse adéquate. Ce colorant, autorisé par la FDA et utilisé pour teinter de nombreux aliments (comme les Cheetos Doritos ou les boissons Kool-Aid), semblait donc sûr pour un usage biologique.
En général, ajouter de la couleur à l'eau la rend moins transparente. Mais ici, la tartrazine absorbe la lumière bleue tout en réduisant le contraste d'indice entre l'eau et les lipides, ce qui permet aux lumières rouge et orange de traverser les tissus sans diffusion — ceux-ci deviennent ainsi transparents dans ces longueurs d'onde. Comme le résume Hong : « Les lipides et l'eau restent chimiquement différents, mais la lumière ne le perçoit plus et les traverse aisément. »
 

Concrètement, après avoir rasé des souris et massé le colorant sur leur peau nue, les chercheurs ont obtenu en quelques secondes une sorte de « vitrail biologique » aux teintes orangées. Ils pouvaient alors observer en direct le battement cardiaque des animaux, ou le transit des aliments dans l'intestin.
À l'aide d'un microscope, l'équipe a aussi examiné d'autres tissus, comme les fibres musculaires d'une patte rasée — ce qui nécessiterait normalement l'implantation d'un endoscope. Ils ont même appliqué le colorant sur le cuir chevelu, le rendant transparent. Associée à un autre colorant fluorescent rouge foncé, cette technique leur a permis d'observer l'activité neuronale dans les couches superficielles du cerveau (le crâne des souris étant naturellement très fin et partiellement translucide).
 

À terme, cette approche pourrait offrir aux chercheurs une fenêtre pour étudier l'activité cérébrale d'un animal en situation naturelle, en pleine exploration ou en train d'effectuer des tâches.Traduction adaptée de Sara Reardon (2024) ici  encourage le lecteur à aller vérifier dans la news d'origine ici ou dans l'article d'origine :  ici

---

Références:

• Auzel, F. (2004). Upconversion and Anti-Stokes Processes with f and d Ions in Solids. Chemical Reviews, 104(1), 139‑174. https://doi.org/10.1021/cr020357g
• Fong, J., Doyle, H. K., Wang, C., Boehm, A. E., Herbeck, S. R., Pandiyan, V. P., Schmidt, B. P., Tiruveedhula, P., Vanston, J. E., Tuten, W. S., Sabesan, R., Roorda, A., & Ng, R. (2025). Novel color via stimulation of individual photoreceptors at population scale. Science Advances, 11(16), eadu1052. https://doi.org/10.1126/sciadv.adu1052
  
• Gibney, E. (2025). Brand-new colour created by tricking human eyes with laser. Nature, 641(8061), 16‑17. https://doi.org/10.1038/d41586-025-01252-3
• Ma, Y., Chen, Y., Wang, S., Chen, Z.-H., Zhang, Y., Huang, L., Zhang, X., Yin, F., Wang, Y., Yang, M., Li, Z., Huang, K., Fang, X., Li, Z., Wang, M., Liu, W., Li, J.-N., Li, L., Zhao, H., … Xue, T. (2025). Near-infrared spatiotemporal color vision in humans enabled by upconversion contact lenses. Cell, S0092867425004544. https://doi.org/10.1016/j.cell.2025.04.019
• Reardon, S. (2024). Slathering mice in a common food dye turns their skin transparent. Science. https://doi.org/10.1126/science.z0idj3h
  
• Solomon, S. G., & Lennie, P. (2007). The machinery of colour vision. Nature Reviews Neuroscience, 8(4), 276‑286. https://doi.org/10.1038/nrn2094
  
• Ou, Z., Duh, Y.-S., Rommelfanger, N. J., Keck, C. H. C., Jiang, S., Brinson, K., Zhao, S., Schmidt, E. L., Wu, X., Yang, F., Cai, B., Cui, H., Qi, W., Wu, S., Tantry, A., Roth, R., Ding, J., Chen, X., Kaltschmidt, J. A., … Hong, G. (2024). Achieving optical transparency in live animals with absorbing molecules. Science, 385(6713), eadm6869. https://doi.org/10.1126/science.adm6869
  
  

G·EM Évasions Mathématiques / les pensées traduites en parole / Pour mémoriser, écrire serait plus efficace que lire

Genève Évasions Mathématiques (G·EM)

 

Genève Évasions Mathématiques (G·EM) est une  structure de l'Université de Genève dédiée à la médiation scientifique en mathématiques qui présente les mathématiques sous un angle favorisant l'inclusion et l'accessibilité à tous les publics. Son activité tourne autour de l'animation, de la création de contenu et de la formation, accueillant des chercheurs et chercheuses, des scolaires et le grand public.

---

Un interface cerveau-machine convertit les pensées en parole, presque en temps réel.

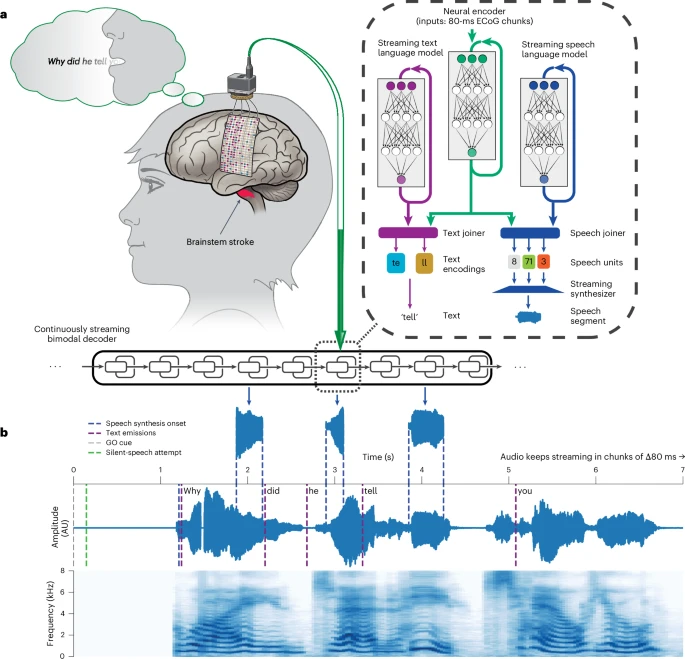"La communication orale naturelle se produit de manière instantanée. Des retards de parole de plus de quelques secondes peuvent perturber le cours naturel d'une conversation. Cela rend difficile la participation des personnes paralysées à un dialogue significatif, pouvant entraîner un sentiment d'isolement et de frustration.Nous avons utilisé des enregistrements de haute densité du cortex sensorimoteur de la parole chez un participant à un essai clinique souffrant de paralysie sévère et d'anarthrie, afin d'alimenter un synthétiseur vocal naturel fonctionnant en flux continu.Nous avons conçu et utilisé des modèles transducteurs de réseaux neuronaux récurrents (deep learning) pour obtenir une synthèse vocale fluide, intelligible et à grand vocabulaire en ligne, personnalisée selon la voix du participant avant la blessure, avec un décodage neuronal toutes les 80 millisecondes.
Hors ligne, les modèles ont démontré une capacité implicite de détection de la parole et pouvaient décoder le discours de manière continue et indéfinie, permettant une utilisation ininterrompue du décodeur et une accélération supplémentaire.
Notre approche s'est également généralisée avec succès à d'autres interfaces de parole silencieuse, incluant les enregistrements à l'unité neuronale et l'électromyographie. Nos résultats introduisent un paradigme de neuroprothèse vocale visant à restaurer une communication orale naturelle chez les personnes atteintes de paralysie."
Traduction de l'abstract encourage le lecteur à aller vérifier dans l'article d'origine :  ici

Video montrant le sujet qui pense et la vocalisation quasi instantanée
https://m.youtube.com/watch?v=MGSoKGGbbXk



Source :

Littlejohn, K. T., Cho, C. J., Liu, J. R., Silva, A. B., Yu, B., Anderson, V. R., Kurtz-Miott, C. M., Brosler, S., Kashyap, A. P., Hallinan, I. P., Shah, A., Tu-Chan, A., Ganguly, K., Moses, D. A., Chang, E. F., & Anumanchipalli, G. K. (2025). A streaming brain-to-voice neuroprosthesis to restore naturalistic communication. Nature Neuroscience, 28(4), 902‑912. https://doi.org/10.1038/s41593-025-01905-6

---

Pour mémoriser, écrire serait  plus efficace que lire

"Afin d'examiner si l'écriture manuscrite présente un avantage dans l'apprentissage de la forme, du son et du sens des mots, cette étude a sélectionné aléatoirement 40 élèves de l'école primaire (20 garçons et 20 filles, âgés de 11,4 ± 1,34 ans). En adoptant une approche expérimentale, nous avons comparé les résultats d'apprentissage à travers trois tâches : l'appariement son-mot, l'appariement sens-mot, et le jugement de forme du mot, dans deux conditions : apprentissage par écriture manuscrite et apprentissage visuel.

Après trois jours consécutifs d'apprentissage et de tests, nous avons constaté que l'écriture manuscrite surperformait généralement l'apprentissage visuel en termes de précision et de temps de réponse dans l'apprentissage de la forme, du son et du sens des mots.

Nous avons également observé des différences dans le moment d'apparition des écarts significatifs entre les deux méthodes selon les trois tâches. Plus précisément, en termes de précision, les écarts sont apparus d'abord dans la tâche d'appariement son-mot dès le premier jour, suivis par la tâche de jugement de la forme, et enfin par celle d'appariement sens-mot. Concernant le temps de réponse, les différences significatives entre les méthodes d'apprentissage ont d'abord émergé dans la tâche de jugement de la forme, puis dans celles d'appariement son-mot et sens-mot.

Ainsi, en combinant les données de précision et de temps de réponse, nous concluons que l'écriture manuscrite est plus avantageuse que l'apprentissage visuel pour l'acquisition de mots, avec un impact différencié selon la forme, le son et le sens des mots, les deux premiers étant priorisés par rapport au sens."
Traduction de l'abstract encourage le lecteur à aller vérifier dans l'article d'origine :  ici

Source :

Y. Ying, et al., The role of handwriting in English word acquisition among elementary students, Acta Psychologica, 2024.

--

Festival Pint of Science 19-21 mai - la science dans un bar ?! Science sans limites mais pinte avec modération

Festival Pint of Science 19-21 mai,

Pint of Science invite certains des scientifiques les plus brillants à venir partager leurs recherches et découvertes les plus récentes dans les bars de votre ville. Aucune connaissance préalable n'est nécessaire : c'est une occasion unique de rencontrer celles et ceux qui façonnent la science de demain. Le festival se tient chaque année pendant trois jours au mois de mai, simultanément dans plus de 400 villes à travers le monde. Pint of Science Suisse est une association à but non lucratif animée par des scientifiques bénévoles et des passionnés de science.  voir About Us ici

à Genève ... 

Science sans limites mais dans la ville de Calvin, pinte avec modération ! à l' I-PUB , Bd Carl-Vogt 20 1205 ici  et au Mr Pickwick Pub Rue de Lausanne 80 1202 ici
Références:

Ailleurs en suisse romande aussi

Pint of science a lieu aussi dans d'autres villes de suisse romande

• Fribourg
• Geneva
• Lausanne
• Neuchâtel
• Sion

"Peut-on vraiment comprendre en comptant ?” par Hugo Duminil-Copin, médaillé Fields, mardi 8 mai

Hugo Duminil-Copin est un conférencier brillant, passionné et passionnant, avec la modestie des grands esprits, qui excelle dans la vulgarisation scientifique.

Ce n'est pas tous les jours qu'on a la chance de pouvoir écouter et discuter avec un lauréat de la médaille Fields (équivalente au Prix Nobel en mathématiques).

Pour vos élèves passionnés, et pour vous faire plaisir !

Conférence tous publics ce mardi soir (18h30) à l' INGE, r. Bartholoni 6, 1204 Genève  1er étage - Les Salons
en replay :  dès le lendemain sur www.inge.ch/replay

Peut-on vraiment comprendre en comptant?

À l'aide d'un exemple emprunté à la recherche du professeur Hugo Duminil-Copin, médaille Fields 2022, nous illustrerons comment compter peut éclairer le comportement de systèmes physiques complexes tout en révélant dans le même temps la nécessité de parfois dépasser ce que nous disent les nombres pour dévoiler tous les mystères du monde qui nous entoure.

Entrée libre. Inscription conseillée ici  Places limitées

Hugo Duminil-Copin

Professeur à l'UNIGE et professeur permanent à l'IHES, médaille Fields 2022

Hugo Duminil-Copin, né en 1985, est un mathématicien français reconnu pour ses travaux novateurs en probabilités et en physique mathématique. Après avoir été nommé professeur assistant à l'Université de Genève en 2013, il devient professeur ordinaire l'année suivante. Depuis 2016, il est également professeur permanent à l'Institut des Hautes Études Scientifiques (IHES). En 2022, il reçoit la médaille Fields, la plus haute distinction en mathématiques. En 2023, il est élu membre de l'Académie des sciences et rejoint le Conseil Présidentiel de la Science.

6 mai 2025 - 18:30  INGE   rue Jean-F. Bartholoni 6, 1204 Genève  1er étage - Les Salons

En outre, la salle est magnifique et facile d'accès (dans le centre de Genève, à deux pas de la place Neuve).

Ce ne serait pas 10 %, mais peut-être seulement 1 ou 2 % des enfants qui ne sont pas génétiquement liés à leur père supposé

Etablir la proportion d'enfants qui ne sont pas du père supposé

La question de la paternité des enfants a toujours été délicate - entre autres parce qu'elle est plus difficile à établir que la maternité. En anglais un dicton ironise : "mother's baby, fathers' maybe".  Faute de données solides, le chiffre de 10 % pour le nombre d'enfants qui ne seraient pas du père supposé a beaucoup circulé.
Une news de Science (Curry, A., 2025) (ici et traduction en pj)) retrace ce chiffre à des estimations des années 90. encourage le lecteur à aller vérifier dans la news d'origine :  ici

Par un des ces hasards qui fleurissent le parcours de la science, en cherchant à authentifier des cheveux de Ludwig van Beethoven avec des techniques génétiques modernes, Maarten Larmuseau a étudié la la filiation masculine de la famille et trouvé que Ludwig n'était pas fils du père supposé. (Peltzer, et al., 2023)(ici)
Larmuseau et al. (2019) (ici) ont développé une méthode, combinant l'analyse des archives généalogiques et les tests ADN sur des individus vivants. Cette approche permet de détecter des cas de paternité inattendue ou mal attribuée, jusqu'à plusieurs siècles en arrière. Il a aussi entrepris une étude à large échelle pour vérifier ce qu'il nomme le taux de paternité extra-paire (EPP) - sans prendre en compte les adoptions connues, les FIV, etc. - dans différentes populations.  D'après (Curry, A., 2025)  encourage le lecteur à aller vérifier dans la news d'origine :  ici

Comment on établit que ce Chromosome Y est le même que celui-là ?

Curry, (2025)  présente le principe de ces techniques, basées sur la filiation direct du chromosome y ( il passe forcément et sans choix de père en fils et donc devrait être le même chez tous les descendants mâles).
Fig 1: ci-contre  [img]. Source :(Curry, A., 2025) (ici)
En recherchant dans les Chromosomes Y séquencés les séquences identiques (IBD) ( voir JTS Comment on analyse l'ADN pour établir une généalogie ou un degré de filiation) C'est ainsi que Maarten Larmuseaua pu établir qu'il y avait eu un cas d'EPP chez les parents de Ludwig ou peu avant. D'après (Curry, A., 2025) encourage le lecteur à aller vérifier dans l'article d'origine (Peltzer, et al., 2023)(ici)

Les découvertes de Larmuseau suggèrent que, malgré les tabous et scandales que peuvent provoquer de tels cas, la paternité hors couple est en réalité assez rare. En effet sur les 500 dernières années, Larmuseau a déterminé que ce taux en Europe est en réalité plutôt 1,5 %. que ce 10%. Et seules quelques cultures assez particulières ont des EPP très différents (il mentionne 48% chez les Himba de Namibie). (Larmuseau,et al., 2013).ici encourage le lecteur à aller vérifier dans la news d'origine :  ici

En fin de compte, ses recherches permettent d'apporter un message clair : « on peut arrêter de paniquer, ce n'est pas le problème que l'on imagine. » encourage le lecteur à aller vérifier dans la news d'origine :  ici

Pourquoi cette question fascine-t-elle tant ?

Curry (2025) évoque divers mécanismes qui pourraient expliquer l'importance accordée à ces EPP. Notamment l'asymétrie de l'investissement parental . "Certains biologistes évolutionnistes ont suggéré que c'est une fonction du fonctionnement de la paternité humaine. Les pères humains investissent de manière exceptionnellement importante dans l'éducation de leurs enfants. En conséquence, l'argument selon lequel les hommes ont évolué pour être particulièrement méfiants envers les enfants nés d'un autre père."  encourage le lecteur à aller vérifier dans la news d'origine :  ici
Voir aussi le cours de prof Maurer à l'UniGE (ici rechercher investissement parental ).

Implications légales

"Ces découvertes ne sont pas seulement d'un intérêt historique. Les identifications médico-légales des victimes d'accidents d'avion ou de catastrophes s'appuient parfois sur la comparaison de l'ADN avec celui de parents vivants. La recherche sur les maladies rares, le conseil génétique et même les antécédents médicaux familiaux standard dépendent d'une généalogie précise pour cartographier les conditions héréditaires, un exercice qui serait presque dénué de sens si le taux d'EPP était de 30 %, voire de 10 %.
Que ce taux soit considérablement plus bas dans la plupart des cultures est une bonne nouvelle pour ces efforts. D'après (Curry, A., 2025)  encourage le lecteur à aller vérifier dans la news d'origine :  ici

Confirmation par l'ADN mitochondrial

Maarten Larmuseau  a ensuite étudié les filiations maternelles (le matériel génétique dans les mitochondries transmis aux enfants provient cette fois seulement de la mère ). Il voulait s'assurer que les cas suspects d'EPP basés sur les chromosomes Y étaient bien ce qu'ils semblaient être : un père non reconnu, et non un cas de bébés échangés entre mères, d'adoption secrète ou de fraude d'identité du 17e siècle, par exemple. « Si je vois des problèmes sur la lignée maternelle, alors je saurais que les changements sur la lignée paternelle n'étaient pas nécessairement de l'EPP », dit Larmuseau.
Y, Larmuseau et son équipe ont alors collecté des échantillons d'ADN de femmes éloignées qui devaient avoir des ancêtres maternels communs pour voir si les généalogies légales correspondaient à la lignée biologique. Après avoir vérifié et re-vérifié les arbres généalogiques maternels de centaines de personnes contre leur ADN mitochondrial, il n'a trouvé aucune surprise. « Cela me donne confiance que les résultats d'EPP que j'ai trouvés sur les pères sont corrects », dit-il. 

D'après (Curry, A., 2025)  encourage le lecteur à aller vérifier dans la news d'origine :  ici

Il faut réfléchir avant de faire un test de paternité …

Cependant, Larmuseau souligne qu'un taux d'EPP de 1 % représente tout de même un grand nombre de personnes. À l'échelle mondiale, environ 30 millions de personnes ont effectué des tests ADN directs aux consommateurs, ce qui signifie qu'environ 300 000 personnes ont peut-être été profondément troublées d'apprendre que leur père biologique n'est pas celui qu'elles attendaient. Ces révélations surviennent souvent sans préparation ni accompagnement, ce que Larmuseau et d'autres estiment être psychologiquement traumatisant.
C'est en partie la raison pour laquelle Larmuseau ne teste pas les frères et sœurs, ni les personnes ayant des parents, grands-parents ou arrière-grands-parents communs, car les conséquences de découvrir un secret familial douloureux dans un passé récent sont trop élevées. Et il offre des séances de conseil aux personnes bouleversées par des découvertes datant d'un siècle ou plus."D'après (Curry, A., 2025)  encourage le lecteur à aller vérifier dans la news d'origine :  ici
Les centres de génétique encouragent aussi à la prudence Voir p. ex  la brochure de la consultation génomique des HUG

(Les membres Jump-To-Science peuvent obtenir ces articles…).

Références:

• Curry, A. (2025). How often are children genetically unrelated to their presumed fathers? Science. https://doi.org/10.1126/science.zp5x60z
• Begg, T. J. A., Schmidt, A., Kocher, A., Larmuseau, M. H. D., Runfeldt, G., Maier, P. A., Wilson, J. D., Barquera, R., Maj, C., Szolek, A., Sager, M., Clayton, S., Peltzer, A., Hui, R., Ronge, J., Reiter, E., Freund, C., Burri, M., Aron, F., … Krause, J. (2023). Genomic analyses of hair from Ludwig van Beethoven. Current Biology, 33(8), 1431-1447.e22. https://doi.org/10.1016/j.cub.2023.02.041
• Larmuseau, M. H. D., Vanoverbeke, J., Van Geystelen, A., Defraene, G., Vanderheyden, N., Matthys, K., Wenseleers, T., & Decorte, R. (2013). Low historical rates of cuckoldry in a Western European human population traced by Y-chromosome and genealogical data. Proceedings of the Royal Society B: Biological Sciences, 280(1772), 20132400. https://doi.org/10.1098/rspb.2013.2400
  
• Larmuseau, M. H. D., van den Berg, P., Claerhout, S., Calafell, F., Boattini, A., Gruyters, L., Vandenbosch, M., Nivelle, K., Decorte, R., & Wenseleers, T. (2019). A Historical-Genetic Reconstruction of Human Extra-Pair Paternity. Current Biology, 29(23), 4102-4107.e7. https://doi.org/10.1016/j.cub.2019.09.07

--

Vous avez manqué une des conférences de la semaine du cerveau 2025 ... tout n'est pas perdu !

(Re)voir les conférences de la semaine du Cerveau 2025

Vous avez manqué les excellents conférences de la semaine du cerveau, ou vous aimeriez en montrer des extraits en classe … 
C'est moins bien qu'en vrai,... mais vous pouvez les revoir par internet. Sur mediaserver depuis ici

Liens directs sur les enregistrements	Bref résumé des conférences
La motivation, moteur de l'adaptation lundi 10 mars 2025 Vieillir: Défis et ajustements mardi 11 mars 2025 Comment vivre avec le numérique mercredi 12 mars 2025 L'intelligence de nos cousins primates jeudi 13 mars 2025

Contact : mona.spiridon@unige.ch

--

Pourquoi ce cercle vicieux démangeaison-gratter-démangeaison

 La démangeaison a un double rôle : pathologique et adaptatif.

 

Dans une news de Science, Emily Underwood (ici) situe le problème : "Toutes les démangeaisons ne disparaissent pas en se grattant. Environ 15 % des individus souffrent de prurit chronique, souvent dû à des pathologies ou à des traitements médicamenteux. Par exemple, les patients atteints de cancer en phase terminale sous morphine ressentent parfois des démangeaisons si intenses qu'ils préfèrent renoncer à l'analgésie.
Des chercheurs ont identifié une hormone chez la souris impliquée dans la transmission du prurit aux neurones de la moelle épinière, relayant ensuite le signal vers le cerveau. Cette découverte pourrait mener à de nouveaux traitements contre le prurit chronique. Elle indique que "Se gratter là où ça démange entraîne un cycle sans fin d'irritation et de soulagement.  Une nouvelle étude éclaire les avantages et les inconvénients de ce phénomène." ça n'explique pas beaucoup les mécanismes biologiques. "Traduction JTS aidé par l'IA encourage le lecteur à aller vérifier dans l'article d'origine :  ici.

Liu,et al. (2025) ici sont plus explicites " Se gratter est un comportement instinctif et conservé (c.-à-d. qu'on le trouve chez de nombreuses espèces, ce qui suggère qu'il aurait été maintenue par sélection au cours de l'évolution) en réponse à la sensation de démangeaison. Dans des maladies comme la dermatite (eczéma), la démangeaison chronique (prurit) est un symptôme majeur qui aggrave l'inflammation. Bien que se gratter intensifie souvent les lésions cutanées, cela procure aussi un soulagement, suggérant un bénéfice [évolutivement] adaptatif." Traduction JTS aidé par l'IA encourage le lecteur à aller vérifier dans l'article d'origine :  ici.

Rationale (ce qu'on ne sait pas encore et que cette recherche tente de comprendre)

Dans la peau, les mastocytes dermiques activés jouent un rôle clé dans la réponse allergique cutanée, provoquant des éruptions et des démangeaisons, ce qui entraîne un comportement de grattage. Les mastocytes recrutent également des cellules inflammatoires et renforcent la défense de l'hôte contre Staphylococcus aureus. Les mastocytes peuvent être activés par divers mécanismes, notamment par des allergènes qui lient les anticorps IgE pré-existantsau récepteur FcεRI (molécules centrales du mécanisme d'activation de la réaction aux parasites - qui s'active à tort lors de l'allergie) , ou encore par la substance P (SP),  un neuropeptide libéré par les neurones sensoriels de la douleurTrpv1 (cf figure 1).

Fig 1: Le grattage agit en synergie avec l'activation des mastocytes via le récepteur FcεRI pour amplifier l'inflammation cutanée allergique. L'interaction des allergènes ou de Staphylococcus aureus avec le récepteur FcεRI ou les IgE sur les mastocytes déclenche la libération de pruritogènes (facteurs induisant la démangeaison), qui sont détectés par les neurones exprimant MrgprA3. Le grattage, provoqué par la sensation de démangeaison, active les neurones exprimant Trpv1, entraînant la libération du neurotransmetteur SP (substance P). La SP, en agissant via le récepteur MrgprB2 sur les mastocytes, potentialise l'activation du FcεRI, augmentant ainsi la libération de TNF par les mastocytes. Cela entraîne une inflammation cutanée accrue et une amélioration de la défense de l'hôte contre S. aureus.  [Figure créée avec BioRender.com]  [img]. Source :Liu,et al. (2025) ici

Les effets de cette activation des mastocytes en réponse aux allergènes et aux infections par Staphylococcus aureus, ainsi que la manière dont le grattage favorise l'inflammation cutanée, et la question de savoir si le grattage est bénéfique pour l'hôte restent mal compris.Traduction JTS aidé par l'IA encourage le lecteur à aller vérifier dans l'article d'origine :  ici.

Fig 2: La bactérie Staphylococcus aureus (rouge et jaune) sur la peau humaine. Credit: Steve Gschmeissner/S  [img]. Source :Sohn, E. (2018).ici:

RÉSULTATS

Emily Underwood (ici) résume : Pour analyser ce cycle, les chercheurs ont appliqué des allergènes sur les oreilles de souris afin d'induire une dermatite, une inflammation cutanée. Certaines souris ont été autorisées à se gratter librement, tandis que d'autres portaient un collier les empêchant d'atteindre leurs oreilles. Les chercheurs ont constaté que les souris capables de se gratter présentaient une inflammation plus marquée et une réponse immunitaire renforcée, mais hébergeaient moins de Staphylococcus aureus, une bactérie pathogène connue pour provoquer des infections cutanées, par rapport aux souris incapables de se gratter. "Traduction JTS aidé par l'IA encourage le lecteur à aller vérifier dans l'article d'origine :  ici.

CONCLUSION

"Le cycle démangeaison-grattage est un processus pathogène dans les éruptions cutanées allergiques, telles que la dermatite ou les réactions aux piqûres d'insectes. Ce cycle amplifie l'inflammation et aggrave la maladie. Nos données suggèrent que le grattage active les neurones cutanés à Trpv1, qui sont une source majeure de Substance P dans la peau. L'activation coordonnée des mastocytes agit en synergie pour renforcer l'inflammation. Ainsi, les mastocytes dermiques jouent un rôle central dans l'inflammation cutanée et sont capables d'intégrer à la fois des signaux neuro-immuns adaptatifs et innés.
De plus, le grattage induit par l'inflammation peut réduire l'abondance de certaines bactéries commensales de la peau et, dans le contexte d'une infection superficielle par S. aureus, l'inflammation déclenchée par le grattage améliore la défense de l'hôte. Ces données illustrent comment le grattage peut à la fois aggraver la maladie et bénéficier à l'hôte via un axe neuro-immunitaire, conciliant ainsi son rôle paradoxal de processus pathologique et d'adaptation évolutive." Traduction et résumé JTS aidé par l'IA encourage le lecteur à aller vérifier dans l'article d'origine :  ici.

PERSPECTIVES

"L'immunologiste Aaron Ver Heul, de la Washington University School of Medicine à St. Louis, qui n'a pas participé à l'étude, déclare à Nature que l'identification du circuit neuronal sous-jacent au « cercle vicieux du grattage » ouvrira la voie à des traitements plus efficaces pour interrompre ce cycle.(ici)

---

(Les membres Jump-To-Science peuvent obtenir ces articles…).

Références:

• Liu, A. W., Zhang, Y. R., Chen, C.-S., Edwards, T. N., Ozyaman, S., Ramcke, T., McKendrick, L. M., Weiss, E. S., Gillis, J. E., Laughlin, C. R., Randhawa, S. K., Phelps, C. M., Kurihara, K., Kang, H. M., Nguyen, S.-L. N., Kim, J., Sheahan, T. D., Ross, S. E., Meisel, M., … Kaplan, D. H. (2025). Scratching promotes allergic inflammation and host defense via neurogenic mast cell activation. Science, 387(6733), eadn9390. https://doi.org/10.1126/science.adn9390
  
• Sohn, E. (2018). Skin microbiota's community effort. Nature, 563(7732), S91‑S93. https://doi.org/10.1038/d41586-018-07432-8
• Underwood, E. (2025). The Secret of the Itch | Science | AAAS. Science. https://doi.org/10.1126/article.25905